立方体 の 体積 を 求める 公式 283580
1
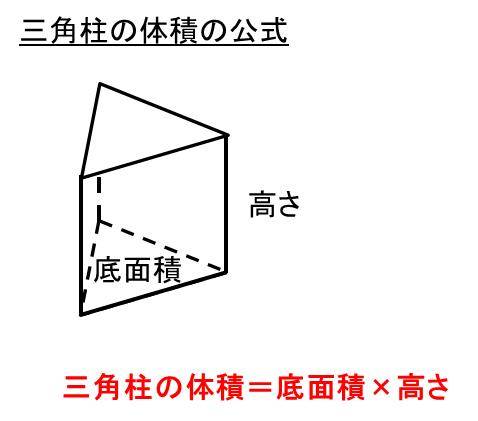
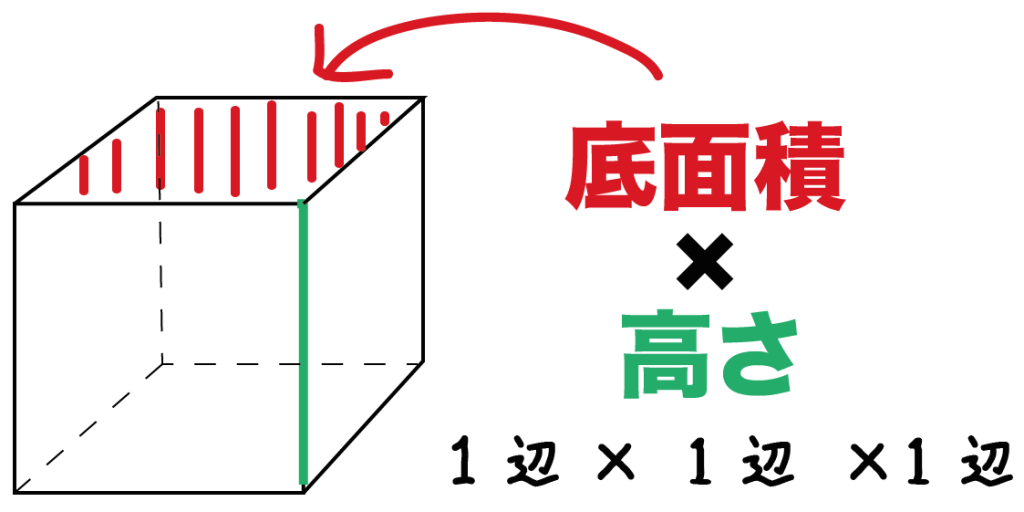
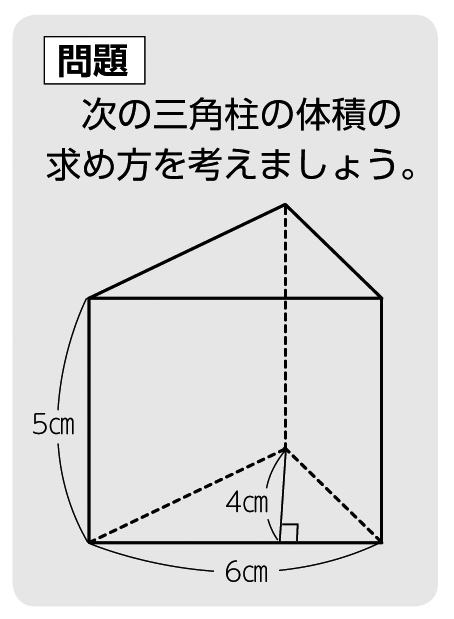
立体の体積 角柱、円柱の体積 柱の体積 = 底面積 × 高さ (例) 三角柱 高さ8cm 底面積 5cm 2 体積=5×8=40 四角柱(直方体) 4cm 3cm 8cm 底面積=4×3=12 体積=12×8=96 半径5cm 高さ 8cm 円柱 底面積=5×5×π=25π 体積=25π×8=0π 例題次の立体の体積を求めよ。 底面積15cm 2, 高さ6cmの五角柱 底面の半径2cm, 高さ10cm立方体の体積=1辺×1辺×1辺 右の図は1辺が40cmの立方体を半径がcmの円柱で たて4cm、よこ4cm、高さ11cmの直方体になる。 求める体積は
立方体 の 体積 を 求める 公式
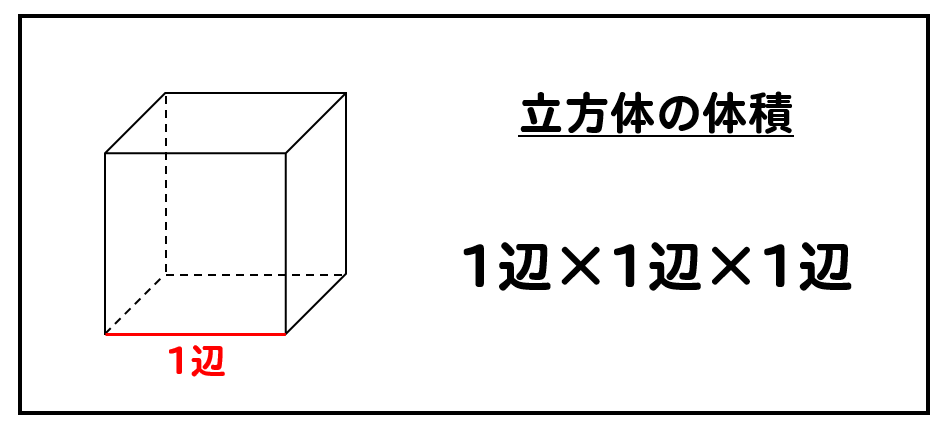
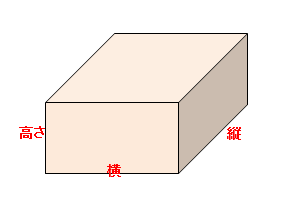
立方体 の 体積 を 求める 公式- 体積が求められるようになると1番最初に扱う立体が、立方体や直方体です。 立方体の体積を求める公式は、「一辺×一辺×一辺」。 直方体の体積を求める公式は、「たて×横×高さ」です。 覚えてしまえば、簡単に体積が求められますが直方体の体積を求める公式を導 き出す。(スマートボードで直方 体を示し、1㎤の数を数える) 「公式を使った答えの求め方」を 練習問題で学習する。 練習問題2問を自力で解く。 立方体の体積を求める公式を導 き出す。(スマートボードで立方

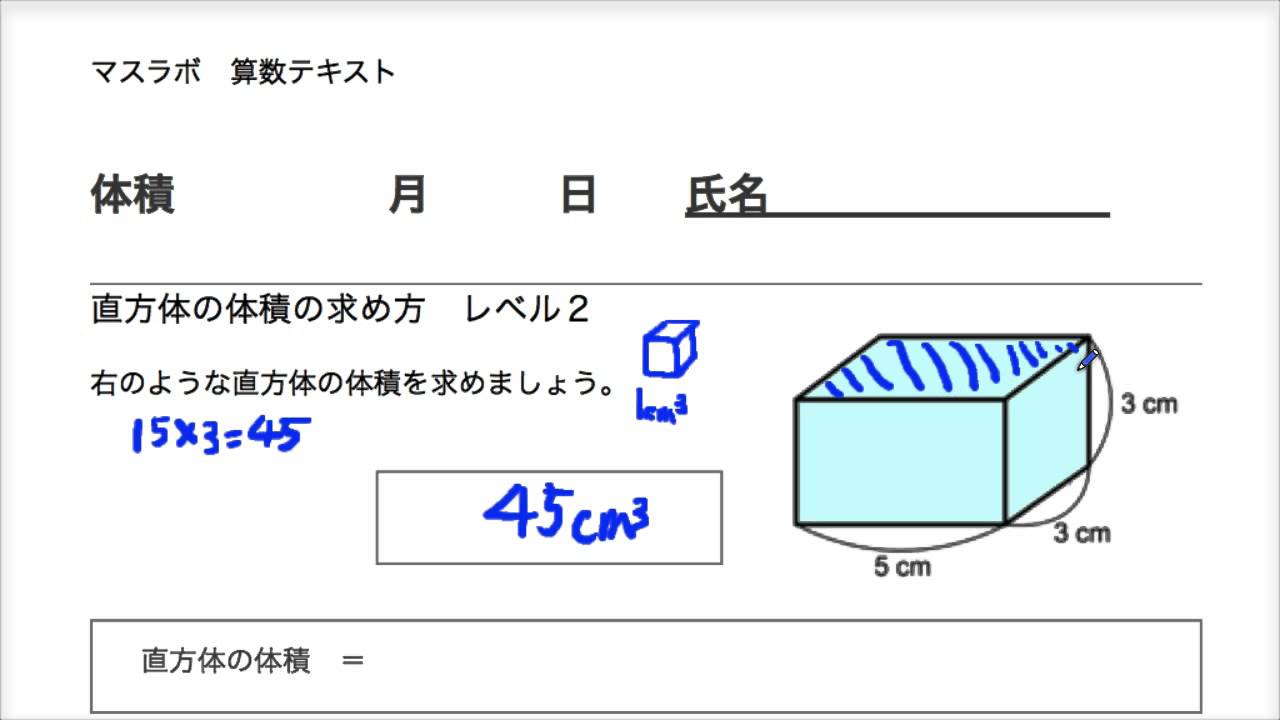
小5 算数 小5 3 直方体と立方体の体積 Youtube
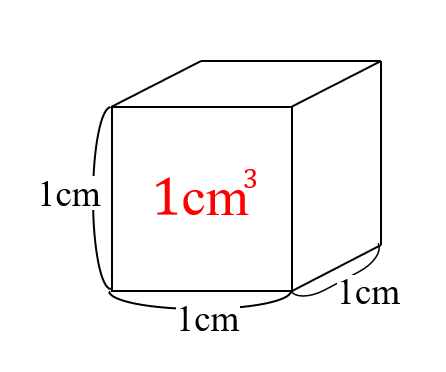
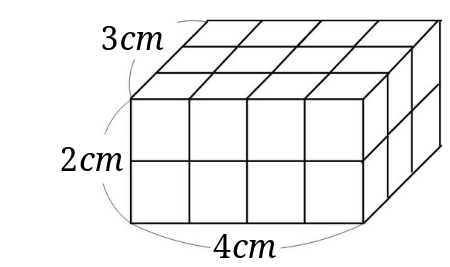
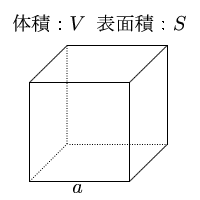
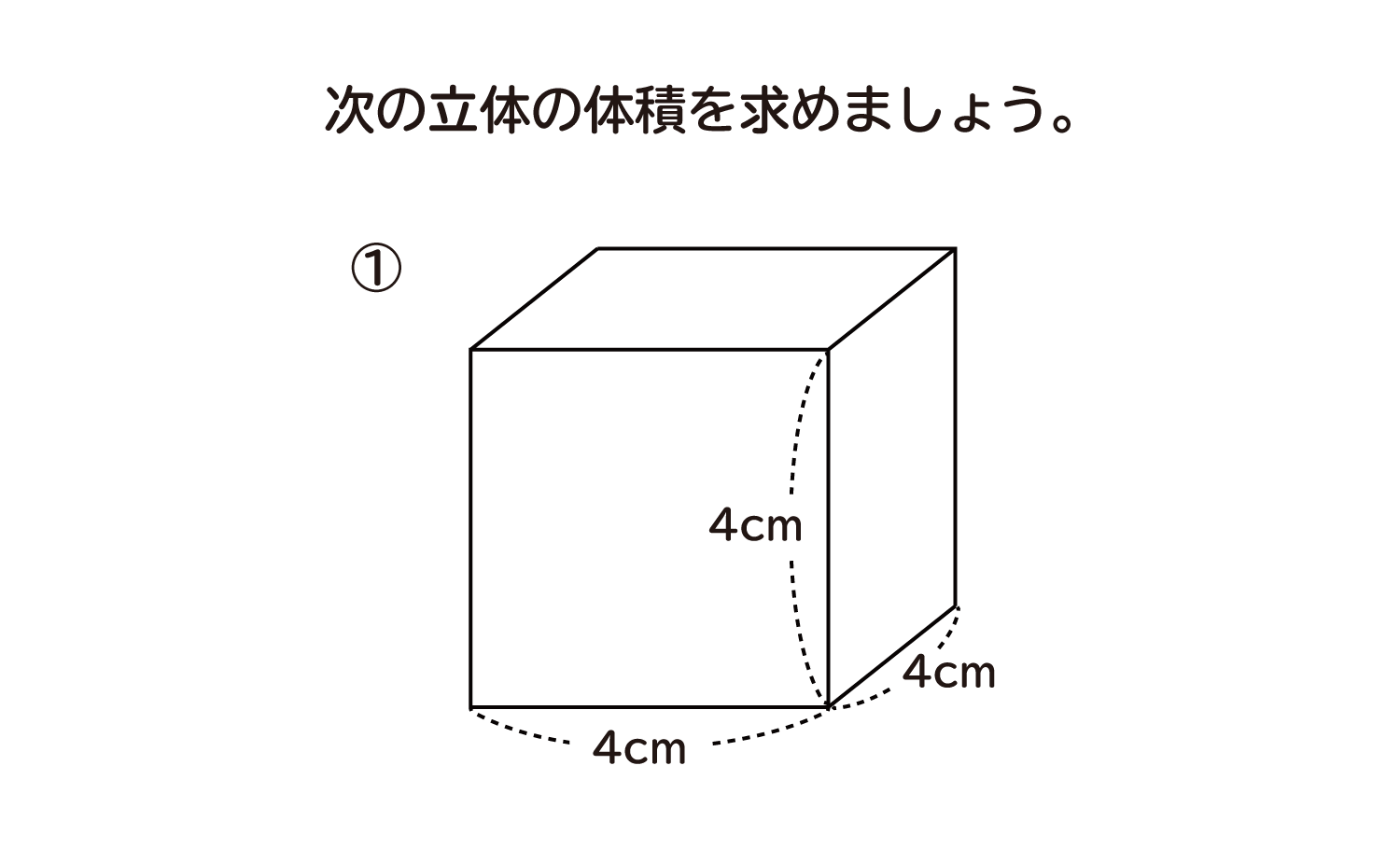
立方体の体積 下図が立方体です。立方体は全ての辺が同じ長さなので、体積の計算も簡単です。縦×横×高さを計算すれば良いですね。 よって、 立方体の体積=4×4×4=64cm 3 です。 立方体の体積は?1分でわかる計算、単位、公式、求め方、リットルとの関係 ③角柱や円柱の体積の公式 ④生活場面での立体の体積を求めるよさ 教え方1 教え方1 5年生で勉強した直方体や立方体の体積の求める公式を生かして、四角柱の体積の求め方を気づかせます。 5年で勉強した立方体と直方体の体積の求め方をふりかえります。1cm 3 が、いくつ入れられるか体積を求める立方体の辺の長さを入力して「計算」ボタンを押してください。 体積を入力して「計算」ボタンを押すと立方体の辺の長さが計算されます。 辺の長さと体積で異なる単位の計算も可能です。 例:辺の長さ500cm=体積125m 3
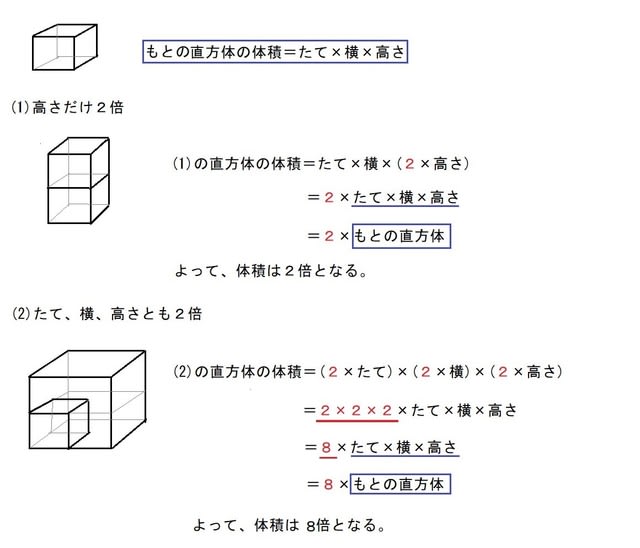
直方体の体積の公式でも 直方体の体積の公式は、たて×横×高さでした。 たて、横、高さは、どれも長さを入れますが、ここを一辺が\(1cm\)の立方体の数を基準にして考えてみましょう。 先ほどの1辺が\(1cm\)の立方体が横に3つ並んだ問題を使いますね。円柱の体積を求める公式は、 V = Sh = πr^2 h で表されます。このページでは、例題と共に、円柱の体積を計算する方法を説明しています。また、斜円柱の体積の求め方も説明しています。 直方体の体積は「縦×横×高さ」じゃなくても求められる どうも、わりと四角四面な一面も持っているジョンです 直方体の体積を求める『縦×横×高さ』 これは小学校で教わる算数の知識で、三つの辺の長さから体積を求める公式です。 例えば、次のよう
立方体 の 体積 を 求める 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
「立方体 の 体積 を 求める 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | |
「立方体 の 体積 を 求める 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「立方体 の 体積 を 求める 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「立方体 の 体積 を 求める 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「立方体 の 体積 を 求める 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「立方体 の 体積 を 求める 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「立方体 の 体積 を 求める 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「立方体 の 体積 を 求める 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「立方体 の 体積 を 求める 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「立方体 の 体積 を 求める 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「立方体 の 体積 を 求める 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
5年算数 体積の教え方1 子どもの学習支援by いっちに算数 体積の勉強は、体積の単位 や を理解させるとわかりやすくなります。 そのために2年「かさ」や4年「直方体と立方体」の勉強を元にして考えさせたいと思います。 忘れているお子さんには、上のリンク先でおさらいさせましょう。本単元は「1 直方体・立方体の体積「2 大きな体積「3 およその形と大き」」 さ」の3つの小単元から構成されている「1 直方体・立方体の体積」では普遍単位。 の必要性を意識し,測定の仕方を考えて体積を求める公式づくりをする「2 大きな。
コメント
コメントを投稿